How to get sick and die in the post-apocalypse
Modeling health conditions in Oregon Road '83
Oregon Road ‘83 is a video game (in development) that is set in the aftermath of a full-scale nuclear war in the early 1980s. As a “simulation game,” it tries to model aspects of what that experience might look like, but within numerous constraints: limited experience, modeling limitations, and the fact that it is meant to be a game, and as such cannot be of such a high complexity that it would require an unreasonable level of attention from the imagined audience.1
Disclaimer: Like the above, much of this post will be highly obvious to people who have designed simulations and games before, or thought about them in a practical way before. But for people who have not, I hope it serves as an interesting overview of the abstract aspects, and I hope that a discussion of the specific practical choices that I made for the game might be interesting to both groups.
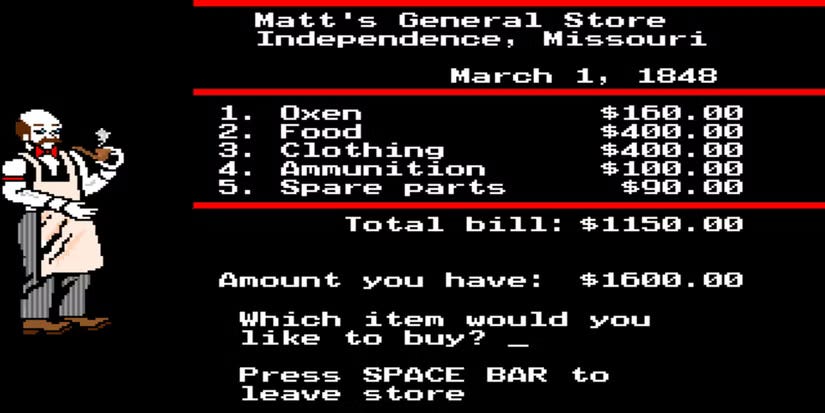
In any "simulation game," there are a limited subset of possible variables that are tracked. In The Oregon Trail (1985), this includes oxen, food, clothing, ammunition, spare parts, and money. The player’s quantity of such items are stored in the game’s memory, and the game’s logic uses these in different ways (food is decreased as a function of time, for example, and spare parts can be used if the wagon breaks down during a random even).
In OR83, food is also tracked as one such variable (but water, however, is not — for the sake of simplifying things as much as possible), because finding adequate stockpiles of food would be a major concern in the first few weeks after such an attack, and its availability or lack thereof would be one of the things that distinguished the circumstances of certain locations from others. But if you are going to track something like food, you have to answer the question: what happens if you run out?
In real life, when we run out of food, we get hungry. This then progresses into starvation, a state that imposes increasingly taxing and unpleasant physiological effects over time, and ultimately, if not addressed, leads to death itself. If we modeled this as simply, "when food = 0, the player dies," it would not feel particularly realistic. Moreover, it would change the nature of food as a variable from real life: it would cease to have much correspondence to the reality of food, and turn it into a totalizing focal point of the player's activity in the game. Which is not what this game's gameplay is meant to be about.
And, on the opposite extreme, if you run out of food and nothing happens to the player or the game, then it is pointless to even track it: it is a variable without meaning, a distinction without a difference.
In between these poles are a wealth of possible options. If one plays games, then several alternatives have already probably come to mind. One that we explored early on was a system of “health points,” often what are called “hit points” in many games. The idea is deceptively simple: create a new variable, called health, and subtract from it while the player is without food, and perhaps replace it when the player consumes food. If it ever reaches 0, the player dies.
This model is an obviously simplification of how reality works, but could be made into a good-enough model with some careful attention to how it is set up. It emphasizes that the hazard of being without food is a prolonged and reversible one, and if one set it up well (the rate of loss and gain), you could imagine it working adequately for hunger. If you wanted it to be more realistic, for example, you might not want the rates of loss and gain to be constant and linear. You might want starvation to be exponential: starts off slow, rapidly speeds up. You might want the rate of recovery to be similarly tailored to the situation being recovered from — perhaps someone who was close to starvation will be slower to recover health than someone who just missed lunch.
But things get messy with the above if you also are modeling other health effects. Radiation exposure at relatively high levels, for example, can produce illness that would synergistically impact the effect of starvation. Should our post-apocalyptic game also model contagious diseases, wounds suffered from misadventures, infections, waterborne parasites? And in what self-respecting homage to The Oregon Trail could one not allow the player to die of dysentery?
These are choices for the game designer, ones with obvious benefits (more realistic, more ways of communicating the education message of what the health and social effects of nuclear war would be) and detrimental (escalating complexity for both the programmers and players).
In Jon Peterson's expansive 2012 history of TSR’s Dungeons & Dragons, Playing at the World, he has an extended discussion of the development of "hit points" as a concept in gaming.2 I found it extremely useful for thinking through the gameplay design issues described above. Many games, like Chess and Checkers, have no such concept: if a knight takes a pawn, the pawn is simply removed from play, “dead.” Hit points first emerged from war gaming simulations that tried to use singular pieces to represent composite units (e.g., a single piece representing a platoon of soldiers) and wanted a way to represent a fractional fighting strength.
As games centered around individual pieces that contained a higher player investment emerged — "hero" pieces in wargaming simulations — the stakes of a piece being "killed" also increased. So "hit points" were used to keep important pieces alive longer than your standard pawn: they are one of several means invented by game designers to help a player “avoid death” in games where a too-easy death makes the game un-fun to play. As anyone who was raised on the early Nintendo games can attest, one-hit kill games are inherently harder than games where your character can soak up a little damage before dying!
Thinking about these matters eventually led me to looking for a very different approach than “health points.” I considered the specific goals that I wanted out of the "health system" of the game:
flexible-enough to model many different sorts of health impacts, including synergistic effects (e.g., radiation poisoning can make otherwise survivable conditions fatal)
detailed-enough to give a sense of the progression of a given disease or health condition
intuitive-enough so that a player would not need to be tracking actual numbers that would not be available to them in the real world to have a sense of their situation and its probable outcomes
accurate-enough that it would not come as a surprise if their character (or an NPC) died or survived a health condition
The above is an admittedly tall bill of order, especially given the desire to keep it intuitive (which argues against high complexity) and also flexible (which argues for high complexity). But it is much easier to design a system built for flexibility if one starts with that goal from the beginning, as opposed to trying to add complexity later to a system that was designed around simplicity.
In thinking about other kinds of “health” systems, one that I found useful is the one in RimWorld, an open-ended science-fiction space colony simulator game (which takes place on a random planet on “the rim of known space”) that is designed around flexibility in the aim of producing emergent behavior. RimWorld’s creator describes it not as a “game” — you cannot “win” in any real sense — but as a “story generator,” in that it creates unusual and unexpected circumstances based on many fairly-complex, non-linear systems that then get a healthy dash of randomness added into them. That’s not quite what OR83 is, but the inherent flexibility of RimWorld’s systems makes it a useful reference point.
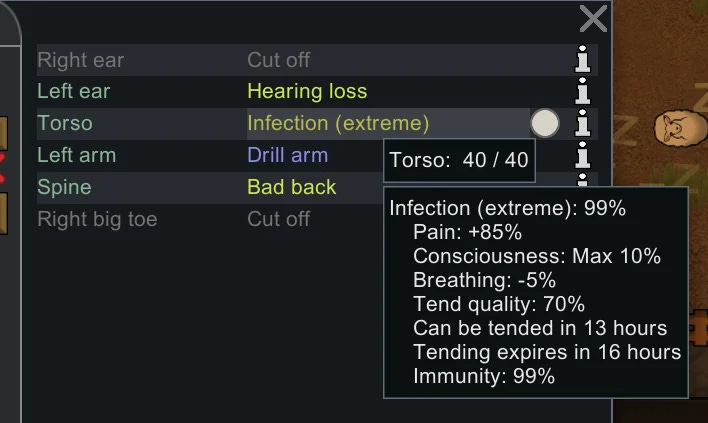
In RimWorld, the “pawns” (the games’ “inhabitants”) all can have different sorts of “status conditions” that include injuries, illnesses, mental states, and so on. These status conditions might be permanent, or only apply if the “pawn” is carrying a certain weapon, or has suffered some kind of condition in the past, or could just be a passing affliction. Each of these conditions has its own set of internal logic to it, and can impact other systems in the game. So “flu” (to just pick one example) is a disease that can affect “pawns” randomly. It normally progresses from 0% to 100%, where 100% is fatal. The “pawn” has an immune system, though, that also counts from 0% to 100%, where 100% is “immune” (which causes the flu’s progress to start counting down). So the disease is really a race between the two counters. By resting and consuming medicine, the “disease” counter’s rate of rise can be slowed, to the point where (ignoring all other possible factors), the “pawn” will gain immunity before the disease kills them. But as the flu’s “disease” counter rises, though, the disease itself has more and more impact on the “pawn,” adding pain, tiredness, lack of coordination, a foul mood, vomiting, and so on. These secondary effects (symptoms) themselves can cause other problems — a “pawn” who vomits while cooking can give other members of the colony food poisoning, for example, and a “pawn” with too foul a mood can have a mental break that causes them to stop responding to the player’s commands (like going to bed and resting).
But one of the main differences between RimWorld and what I wanted to make is that in RimWorld there is an assumption that the player wants to be awash in data and complexity and act upon it very specifically. There are a lot of numbers. With OR83, I wanted something that would have almost no visible numbers, but still make a lot of sense to a player, and allow them to be able to make choices based on the information they do have, without worrying about “gaming” the system underneath it. Which is tough, if you have a system (like RimWorld’s) where the numbers aren’t entirely intuitive (at least, they aren’t for me).
For OR83, what evolved out of all of this is really two systems. One is a generic system internally called the “check” system, which is what runs after any time has passed in-game. So if an event has occurred that caused 30 minutes to pass, that time is sent along to the “check” system, which then takes care of a number of time-based subsystems, like checking on whether the player or NPC is hungry-enough to eat, adding any accumulated radiation to their internal counters, checking if they need to sleep, and so on.

One of these systems that falls under the “check” system is the “conditions” system, which monitors the progress of different health or status conditions. Each of these “conditions” is a little code module that tracks how the condition should be changing over time. So, for example, the “food” system might determine that a certain amount of time has passed since the player last ate, and that it is an appropriate time of the day to eat again (so the player can ration food if they want, and not just continuously be snacking every time they get hungry), and if they have food to eat. If everything lines up correctly, they eat some amount of food and that resets their counter for having eaten. (There is more that can happen here — e.g., if you have set it to only eat half as much food, it might only reset it by half.) If they don’t have food, it adds a condition called “hungry” to the player’s internal state.
The “hungry” condition doesn’t do much at first, but can add a small status icon that indicates that the player (or NPC) is hungry. If the actual human player investigates the status of their character (or NPC), there will be a line of text that notes that they are hungry.
As more time goes by in-game, the “hungry” code updates its own internal counter. After it meets a certain threshold, “hungry” removes itself and adds “star” in its place. To be “starving” is much worse than being “hungry”: as it progresses, it goes through different “stages” that are taken from standard medical texts about the actual stages of starvation. Every time a new “stage” is reached (each “stage” is defined by some number of hours), a warning message is sent to the player that describes the sensations associated with the starvation. Additional variables, like a general “natural healing factor,” can be negatively impacted by different stages of “starving” (which can affect other health conditions). An NPC’s mood can be negatively affected, too, leading to other effects (if an NPC gets too low, they can do a variety of things, depending on how they are programmed, ranging from abandonment to, uh, murder).
And if “hungry” or “starving” detect that a player has eaten food, however, then they can remove themselves. But it’s all arbitrary code, so you can have a disease that, say, only removes itself after a certain amount of time, or never removes itself, or requires antibiotics, or randomly goes away, or even spreads to other NPCs in your group.
Rather than have some kind of hard cutoff for how a disease kills a player or NPC (a simple counter approach), OR83 uses an internal variable called “severity” that all conditions contribute to every time its “check” code is run. After all conditions have been “checked,” the “severity” contribution from all of them is summed, and is a number between 0 and 100. This is not a linear counter to death, but rather is a probabilistic measure of the odds of them dying on a given day. A severity of 0 always means that they have a 0% chance of dying, and a severity of 100 always means they have a 100% chance of dying, but the other probabilities are distributed on the basis of an exponential equation that uses a constant to determine the probability of death. With a “severity constant” of 10,000, for example, this is warped in a way so that until “severity” is equal to at least 50, the chance of death per day is effectively 0%. After that, the chance starts to rise: about 1% at 60; 3% at 70; 10% at 80; 32% at 90; 56% at 95, etc. With different constants, you have a different mapping:3
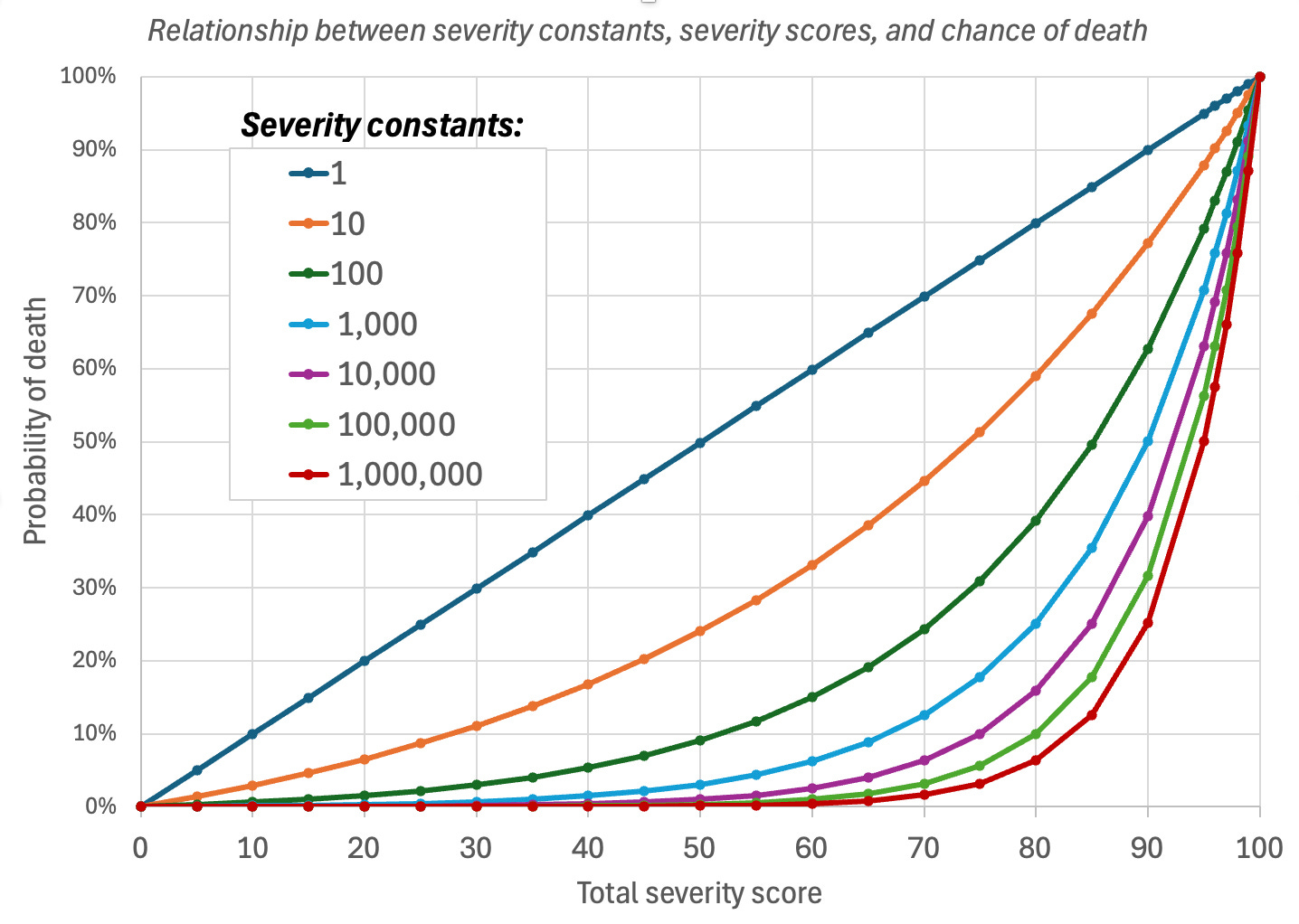
What I like about this exponential approach is that it seems like it reflects reality a bit better — you can have a lot of little things chipping away at someone, and they might die from the sum total of them, but the odds aren’t super high in any given day that this might occur. But if they are really suffering from either a major health problem, or a combination of factors, then that chance might rise. (And in the “check” function, this “probability per day” is of course translated into whatever unit of time is being “checked.”)
We’re still tweaking these numbers, but I appreciate (as a not-very-mathematical person) that with an equatin like this, you can jus change one constant to easily tweak the probabilities. So if it turns out that the health system feels unintuitive (goes from “nothing” to “dead” too quickly), the whole thing can be shifted as a whole, or individually for any given “condition.”
How this will all work out in the final version (or even beta version) remains to be seen, but the process of thinking through how to model all of this was very generative for me, and led to a framework that feels like it could lead to outcomes that would feel intuitive for a player, as well as giving enough flexibility and modularity that, as a programmer and designer, it can be adapted to all sorts of different outcomes.
I use “simulation game” here in the specific style of R. Philip Bouchard, lead designer of The Oregon Trail (MECC, 1985) and author of You Have Died of Dysentery: The creation of The Oregon Trail (2016), which is an excellent discussion of the game’s development and philosophy. He has an excellent chapter on modeling (“Building the Mathematical Models”) which I would recommend to anyone interested in thinking about “simulation games” in general. I would also note that “how much complexity is the right amount of complexity?” is not an easy question to answer, even for a game meant for a relatively large audience — people are quite capable of juggling a lot of information under the right circumstances, if they are inclined to do so. Indeed, many people find that very compelling.
Jon Peterson, Playing at the World: A History of Simulating Wars, People and Fantastical Adventures, from Chess to Role-Playing Games (Unreason Press, 2012), chapter 3.2.2 (“Avoiding Death: Hit Points, Armor Class, and Saving Throws”). Peterson’s excellent book has been reissued in a new edition by MIT Press recently, but broken into two volumes, and I am not sure exactly where in the new layout this chapter or its equivalent is contained. My sense is that it may not be until the second volume? It is hard to tell from the table of contents that has been published for the second edition, which retains parts of the original structure, but does not seem to contain what was chapter 3 (“System – The Rules of the Game”) of the previous edition.
For those who are interested in even more details, the equation takes the basic form of p = (n^(s/100)-1)/(n-1); where: p = probability of death (0–1), n = constant (in the above examples); s = severity level (0-100). By changing n, one gets a very different shape of the graph. In the above equation, n cannot be equal to 1 without a divide-by-zero error, but I have set up the actual function in the code to detect this case, and regard that n=1 as a linear relationship (50 in = 50% out). If n>1, the probability rises exponentially with increasing severity; if n<1, then the probability rises fast but then plateaus. This general way to get a quick mapping of a linear number to an exponential probability distribution is very flexible and used for a number of other systems in the OR83 game that rely on non-linear relationships. I don’t recall exactly where I found this equation (I am sure I did not invent it), but my very non-mathematical understanding is that it not an uncommon form of exponential formula. ChatGPT suggests that it could be considered a specific case of the “partial sum formula” of the geometric series, for whatever that is worth!


Alex, Did you see the piece in the NYT magazine this week about the Proud Prophet war game in 1983?
Excellent rundown of games and game math.. I gotta apply this to algorithms in a game app